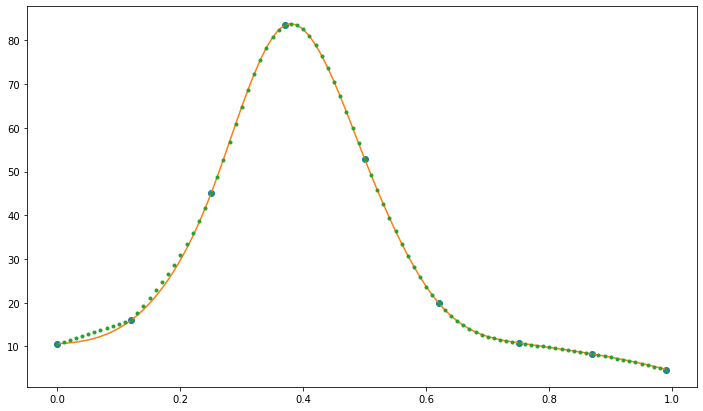
Spline Fit
""" From "COMPUTATIONAL PHYSICS", 3rd Ed, Enlarged Python eTextBook
by RH Landau, MJ Paez, and CC Bordeianu
Copyright Wiley-VCH Verlag GmbH & Co. KGaA, Berlin; Copyright R Landau,
Oregon State Unv, MJ Paez, Univ Antioquia, C Bordeianu, Univ Bucharest, 2015.
Support by National Science Foundation"""
# SplineInteract.py Spline fit
import matplotlib.pyplot as plt
import numpy as np
x = np.array([0.0, 0.12, 0.25, 0.37, 0.5, 0.62, 0.75, 0.87, 0.99]) # input
y = np.array([10.6, 16.0, 45.0, 83.5, 52.8, 19.9, 10.8, 8.25, 4.7])
n = 9
# Initialize
y2 = np.zeros_like(y)
u = np.zeros_like(y)
Nfit = 100 # Original algorithm did Nfit + 1 points instead
Xfit = np.zeros((Nfit), float)
Yfit = np.zeros((Nfit), float)
yp1 = (
(y[1] - y[0]) / (x[1] - x[0])
- (y[2] - y[1]) / (x[2] - x[1])
+ (y[2] - y[0]) / (x[2] - x[0])
)
ypn = (
(y[-1] - y[-2]) / (x[-1] - x[-2])
- (y[-2] - y[-3]) / (x[-2] - x[-3])
+ (y[-1] - y[-3]) / (x[-1] - x[-3])
)
if yp1 > 0.99e30:
y2[0] = 0.0
u[0] = 0.0
else:
y2[0] = -0.5
u[0] = 3 / (x[1] - x[0]) * ((y[1] - y[0]) / (x[1] - x[0]) - yp1)
for i in range(1, n - 1): # Decomp loop
sig = (x[i] - x[i - 1]) / (x[i + 1] - x[i - 1])
p = sig * y2[i - 1] + 2.0
y2[i] = (sig - 1.0) / p
u[i] = (y[i + 1] - y[i]) / (x[i + 1] - x[i]) - (y[i] - y[i - 1]) / (x[i] - x[i - 1])
u[i] = (6.0 * u[i] / (x[i + 1] - x[i - 1]) - sig * u[i - 1]) / p
if ypn > 0.99e30: # Test for natural
qn = un = 0.0
else:
qn = 0.5
un = 3 / (x[-1] - x[-2]) * (ypn - (y[-1] - y[-2]) / (x[-1] - x[-2]))
y2[-1] = (un - qn * u[-2]) / (qn * y2[-2] + 1)
for k in range(n - 2, 1, -1):
y2[k] = y2[k] * y2[k + 1] + u[k]
for i in range(Nfit): # Begin fit
xout = x[0] + (x[-1] - x[0]) * i / (Nfit - 1)
klo = 0 # Bisection algor
khi = n - 1
while khi - klo > 1:
k = khi + klo >> 1
if x[k] > xout:
khi = k
else:
klo = k
h = x[khi] - x[klo]
if x[k] > xout:
khi = k
else:
klo = k
h = x[khi] - x[klo]
a = (x[khi] - xout) / h
b = (xout - x[klo]) / h
yout = (
a * y[klo]
+ b * y[khi]
+ ((a * a * a - a) * y2[klo] + (b * b * b - b) * y2[khi]) * h * h / 6
)
Xfit[i] = xout
Yfit[i] = yout
from scipy.interpolate import CubicSpline
plt.figure(figsize=(12, 7))
plt.plot(x, y, "o")
plt.plot(Xfit, CubicSpline(x, y)(Xfit), "-")
plt.plot(Xfit, Yfit, ".")
plt.show()